|
摘要:在用
SPC
進行質量控制的過程中, 其核心是對產品進行合理分組抽樣后, 再進行的質量特性數據的分析.正態分布已經貫穿整個質量特性數據分析的過程, 是進行質量控制的最重要的工具.
正態分布
正態分布是指變量的頻數或頻率呈中間最多,兩端 逐漸對稱地減少,表現為鐘形的一種概率分布。從理論上說,若隨機變量x的概率密度函數為:
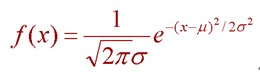
則稱x服從均數為μ,標準差為σ2的正態分布。
正態分布的特點
•
正態分布有兩個參數(parameter),即位置參數(均數)和變異度參數(標準差)。
•
高峰在均數處;
•
均數兩側完全對稱。
•
正態曲線下的面積分布有一定的規律。
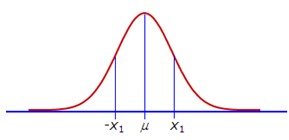
•
X軸與正態曲線所夾面積恒等于1 。
•
對稱區域面積相等。
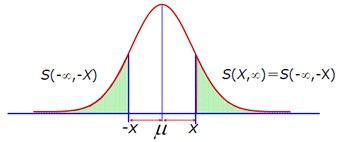
正態曲線下面積的分布規律
•
正態曲線下面積的意義:正態曲線下一定區間內的面積代表變量值落在該區間的概率。整個曲線下的面積為1,代表總概率為1。
•
曲線下面積的求法:定積分法和標準正態分布法
正態分布曲線下的面積
•
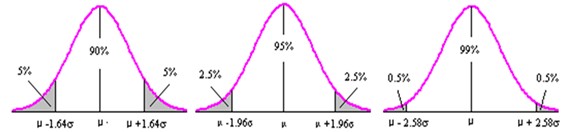
μ±σ范圍內的面積為68.27%
•
μ±1.96σ范圍內的面積為95%
•
μ±2.58σ范圍內的面積占99%
正態分布在質量控制中的意義
當我們運用正態分布曲線、直方圖、
控制圖
等工具對質量特性數據進行分析和控制時,正態分布是其中最為關鍵的工具,因為在正常情況下產品質量特性值的分布,一般都服從正態分布或近似正態分布;并且在控制圖的使用上,也要求抽樣數據符合正態分布作為前提;在最后進行的過程能力分析時也必須符合先要達到正態分布這個條件.所以正態分布已經貫穿整個質量特性數據分析的過程.
符合正態分布的事物在日常生活中是普遍存在的,它具有一定的廣泛性.正態分布在對產品的質量特性數據的分析過程中占有重要的地位.在運用正態分布檢驗質量特性時,可以以它為基礎,并在此基礎上構筑出高效實用的檢驗方法和檢驗步驟,這為
SPC
的發展和應用打下了堅實的基礎.
|